Иллюстрированный самоучитель по Mathematica
Вычисление интегралов
Вычисление интегралов в символьном виде
Одна из важнейших операций — вычисление первообразных и определенных интегралов в символьном виде. Первообразная — это функция F(x), удовлетворяющая уравнению

где С — постоянная интегрирования. А вычисление определенного интеграла с пределами — верхним b и нижним а — производится по формуле

Заметим, что определенный интеграл может быть представлен как аналитическим, так « численным значением. Для вычисления численных значений определенных интегралов разработан ряд приближенных методов — от простых (прямоугольников и трапеций) до сложных, автоматически адаптирующихся к характеру изменения подынтегральной функции f(x).
Для интегрирования в системе Mathematica используются следующие функции:
- Integrate [f, x] — возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х;
- Integrate [f, {x, xmin, xmax}] — возвращает значение определенного интеграла с пределами от x min до x max ;
- Integrate [f, {x, xmin, xmax}, {у, ymin, ymax},...] —возвращает значение кратного интеграла с пределами от x min до x max по переменной х, от y min до y max по переменной у и т. д. (кратность реально не ограничена).
Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции:
Options[Integrate]
{Assumptions -> {}, GenerateConditions->Automatic,
PrincipalValue > False)
Для обозначения бесконечных пределов используется константа Infinity. Эта константа означает положительную бесконечность, для задания отрицательной бесконечности она используется со знаком «минус». Пределы могут задаваться как константами, так и функциями.
Особый интерес, естественно, вызывает применение функции Integrate для вычисления заданных пользователем неопределенных интегралов в символьном виде. Это иллюстрируют примеры на вычисление неопределенных интегралов с алгебраическими подынтегральными функциями, представленные на рис. 4.2.
Здесь входная ячейка в первом примере представлена в формате ввода (Input-Form), а в остальных примерах — в стандартном формате (StandardForm). При записи интегралов последний предпочтителен ввиду большей наглядности, поскольку при этом знаки интеграла имеют естественный математический вид. Обратите внимание на проверку операции интегрирования с помощью дифференцирования в двух последних примерах.
На рис. 4.3 показано еще несколько примеров вычисления неопределенных интегралов. Нетрудно заметить, что интегралы от ряда алгебраических функций дают выражения с тригонометрическими функциями.
Другая группа примеров, представленная на рис. 4.4, показывает нахождение интегралов с тригонометрическими и гиперболическими подынтегральными функциями.
Последний пример показывает, что возможно вычисление списка определенных интегралов, если подынтегральные функции представлены также в виде списка.

Рис. 4.2. Примеры вычисления неопределенных интегралов (начало)
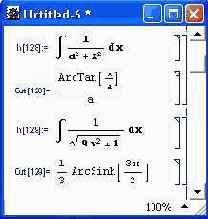
Рис. 4.3. Примеры вычисления неопределенных интегралов (продолжение)
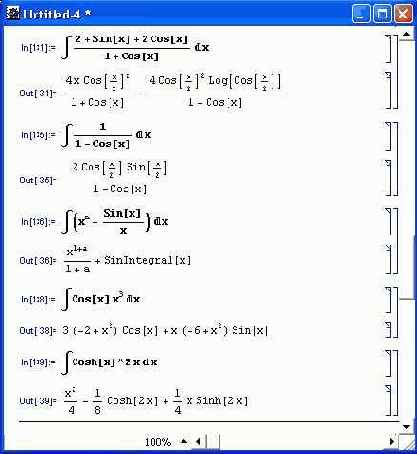
Рис. 4.4. Примеры вычисления неопределенных интегралов (окончание)
