Иллюстрированный самоучитель по Mathematica
Поиск корней уравнений
Для вычисления корней полиномиальных уравнений используется функция Roots:
Roots[lhs==rhs, var]
На рис. 4.18 представлены примеры применения функции Roots.
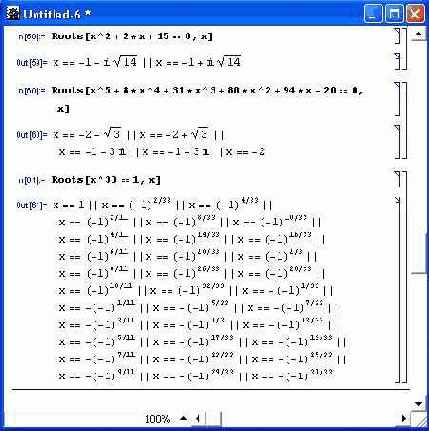
Рис. 4.18. Примеры использования функции Roots
Формат выдачи результатов для функции Roots отличается от такового для функции Solve. Поэтому проверку решения подстановкой надо выполнять как в следующем примере:
e = x^2+3x==2
Зх + х2 == 2
N[Roots[e, x]]
х == -3.56155 | | х == 0.561553
r= {ToRules[%]}
{{х^-3.56155}, {х^ 0.561553}}
е/. r
{True, True}
Для преобразования результата вычислений в список решений (подобный решениям, получаемым с помощью функции Solve) здесь использована функция ToRules.
При затруднениях в решении уравнений с помощью функции Roots можно использовать следующие опции:
Options[Roots]
{Cubics -> True, Eliminate -> False, EquatedTo-> Null,
Modulus -> 0, Multiplicity->1, Quar tics -> True, Using -> True}
Ниже они описаны подробно:
- Cubics — указывает, следует ли искать явные решения для неприводимых кубических уравнений;
- EquatedTo — задает выражение для замещения переменной в решении;
- Modulus — задает промежуточную факторизацию полинома;
- Multiplicity— устанавливает кратность каждого из корней в конечном результате;
- Quartics — задает точное решение квадратного уравнения и полинома четвертой степени;
- Using — указывает какие-либо дополнительные уравнения, которые следует использовать для решения уравнений.
Применение опций нередко позволяет получать решения, которые не удаются с первого раза. Однако это требует определенного опыта и понимания сути решаемой задачи.
